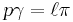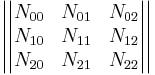Configuration (geometry)

In mathematics, specifically projective geometry, a configuration in the plane consists of a finite set of points, and a finite arrangement of lines, such that each point is incident to the same number of lines and each line is incident to the same number of points.

Although certain specific configurations had been studied earlier (for instance by Thomas Kirkman in 1849), the formal study of configurations was first introduced by Theodor Reye in 1876, in the second edition of his book Geometrie der Lage, in the context of a discussion of Desargues' theorem. Ernst Steinitz wrote his dissertation on the subject in 1894, and they were popularized by Hilbert and Cohn-Vossen's 1932 book Anschauliche Geometrie (reprinted in English as Geometry and the Imagination).

Configurations may be studied either as concrete sets of points and lines in a specific geometry, such as the Euclidean or projective planes, or as abstract incidence structures. In the latter case they are closely related to regular hypergraphs and regular bipartite graphs.

Contents

Notation

A configuration in the plane is denoted by (pγ ℓπ), where p is the number of points, ℓ the number of lines, γ the number of lines per point, and π the number of points per line. These numbers necessarily satisfy the equation

p\gamma = \ell\pi\,

as this product is the number of point-line incidences.

The notation (pγ ℓπ) does not determine a projective configuration up to incidence isomorphism. For instance, there exist three different (93 93) configurations: the Pappus configuration and two less notable configurations.

For some configurations, p = ℓ and γ = π, so the notation is often condensed to avoid repetition. For example (93 93) abbreviates to (93).

Examples

Notable projective configurations include the following:

Duality of configurations

The projective dual to a configuration (pγ lπ) is a configuration (lπ pγ). Thus, types of configurations come in dual pairs, except when p = l and the configuration type is self-dual.

The number of (n3) configurations

The number of nonisomorphic configurations of type (n3), starting at n = 7, is given by the sequence

1, 1, 3, 10, 31, 229, 2036, 21399, 245342, ... (sequence A001403 in OEIS)

These numbers count configurations as abstract incidence structures, regardless of realizability (Betten, Brinkmann & Pisanski 2000). As Gropp (1997) discusses, nine of the ten (103) configurations, and all of the (113) and (123) configurations, are realizable in the Euclidean plane, but for each n ≥ 16 there is at least one nonrealizable (n3) configuration. Gropp also points out a long-lasting error in this sequence: an 1895 paper attempted to list all (123) configurations, and found 228 of them, but the 229th configuration was not discovered until 1988.

Higher dimensions

The concept of a configuration may be generalized to higher dimensions, for instance to points and lines or planes in space. Notable three-dimensional configurations are the Möbius configuration, consisting of two mutually inscribed tetrahedra, Reye's configuration, consisting of twelve points and twelve planes, with six points per plane and six planes per point, the Gray configuration consisting of a 3×3×3 grid of 27 points and the 27 orthogonal lines through them, and the Schläfli double six, a configuration with 30 points, 12 lines, two lines per point, and five points per line.

A further generalization is obtained in three dimensions by considering incidences of points, lines and planes, or j-spaces (0 ≥ j > 3), where each j-space is incident with Njk k-spaces (j ≠ k). Writing 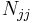N_{jj} for the number of j-spaces present. a given configuration may be represented by the matrix:

\begin{vmatrix}\begin{vmatrix}N_{00} & N_{01} & N_{02} \\ N_{10} & N_{11} & N_{12} \\ N_{20} & N_{21} & N_{22}\end{vmatrix}\end{vmatrix}

The principle extends generally to n dimensions, where 0 ≥ j > n. Such configurations are related mathematically to regular polytopes (Coxeter 1948).

References

External links